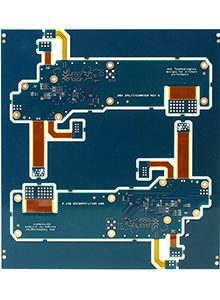
Multi layer Boards
Multilayer 4-50L≥$140/㎡Rigid Flex PCB
5days Delivery≥$135/㎡BOM Procurement
100% original
≥$50/sample
PCB Assembly
Full Turn-Key PCB Assembly
2-4 days Delivery
ABOUT Fast Turn PCB
FAST TURN PCB founded in 2015Y, We have one PCB factory and one PCB assembly factory ,have about 350 employees, We Focus on PCB & PCBA Turnkey solution, Good at small & medium-sized volume, quick turn delivery, we committed to Provide high reliability products to our customer .80% of our products are sold to Europe and America,20% are sold to Asia and domestic, widely used in medical,industrial control,Telecom communication and semiconductor etc.
PCB factory Good at multi-layer PCB (4-50 layers), HDI blind & buried board, High frequency material board, Rigid-flex board, certificated by ISO 9001, UL(E520899), Rohs & Reach. Every pcb board will do 100% inner and outer layer AOI, E-test, via hole wall test etc.
PCBA factory owns capability on BGA, QFN, 0201, 01005; has Quality control equipment like SPI system, AOI, first-piece inspection, X-Ray and so on.
Our Target is to provide “Reliable Quality, Quick Delivery, Professional Service and Fair Pricing”.
PCB Manufacturing,PCB Assembly, Circuit Maker-Fast Turn PCb
Are you looking for a high-quality and full-range PCB fabrication, PCB assembly, and components sourcing services? Then, Fast Turn PCB is here to provide your needs at affordable rates. Yes, you read it right! Our company has been in the industry for many years, guaranteeing the best products and services you will surely love!
Who We Are
A renowned manufacturer in China, Fast Turn PCB is a one stop shop that can provide everything your company needs as far as PCB products and services are concerned. Our company values our customers and thereby never fails to meet your standards and needs.

Our Advantage
Multi-layers 4-10 layers Expedited 2-3 days delivery
HDI PCB Rush Service 5-7 Days
SMT Prototype Rush Service 1-3 Days
Component Purchase Insure parts is original
Difficuit board We have team Work for it
PCB Design 15 years layout 50+ design team
Multi-layers 4-10 layers Expedited 2-3 days delivery
HDI PCB rush service 5-7 Days
SMT prototype rush service 1-3 Days
Ensure that component procurement is original
Difficuit board we have specialized team work for it
PCB design 15 years layout 50+ design team
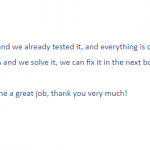
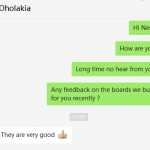
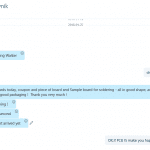
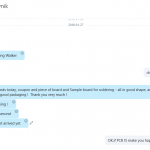
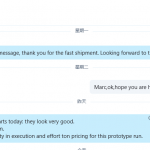
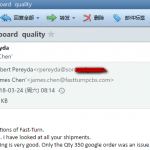
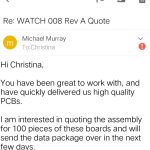
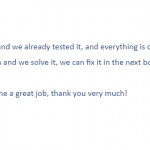
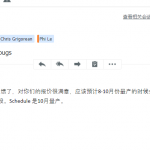
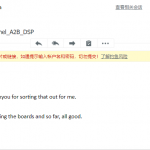
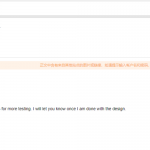
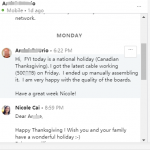
Customer Testimonials



News

8 Various Factors Influencing PCB Board Prices
1: Materials used for PCB Taking ordinary double-sided boards as an example, the board material generally includes FR4, with thicknesses ranging from 0.2mm to 3.0mm and copper thicknesses ranging from

Why choose one-stop PCB Assembly services
Electronics manufacturers need a dependable partner to supply the electronic chip that goes into all our smart electronic gadgets. Whether it’s a luxury car or smartwatch, a remote-controlled child’s

Analysis of the causes and avoidance measures for 9 major defects in PCB boards
1. Poor substrate and leakage of the bottom plate may cause scratches during transportation, resulting in circuit gaps. Easy to affect the impedance of product wiring. Standardize homework and strengt

How to layout special PCB components
In PCB design, we often encounter a variety of PCB special components, and the layout of these special components also has many considerations. Today, we will introduce how to layout PCB special compo

Requirements for flatness, curvature and distortion of PCB circuit boards
Let’s take a look at the concept of flatness and quality control issues of PCB circuit boards together. The flatness of PCB printed boards is determined by two characteristics of the product: cu

The industry trend of PCB circuit boards is becoming more diversified and specialized
With the continuous progress of technology, PCB (printed circuit board), as the core component of electronic products, has attracted widespread attention from the industry in its development trend. Th